https://school.programmers.co.kr/learn/courses/30/lessons/42895
문제 정의
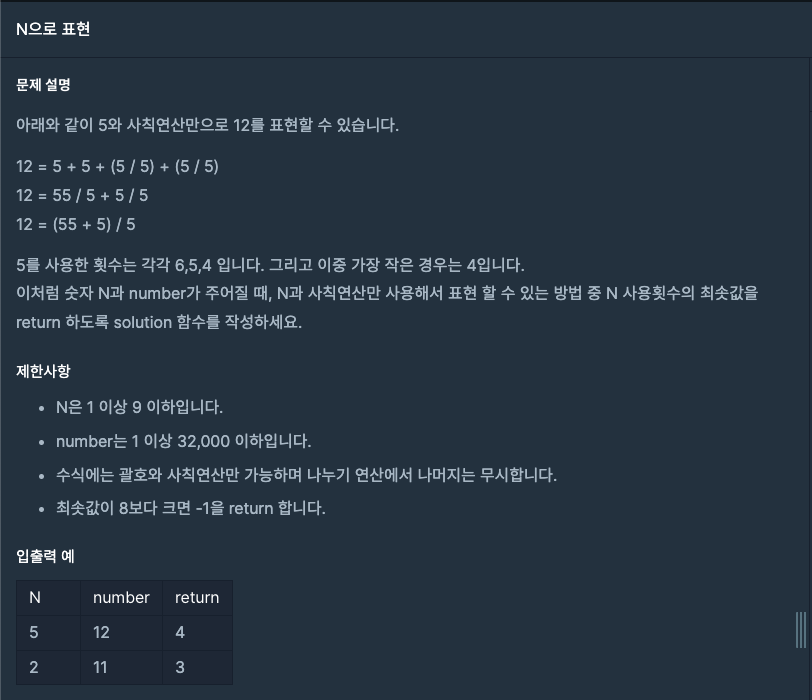
어떤 숫자 N과 numbers가 주어질 때, N과 사칙연산만 사용해서 numbers를 표현해야 한다.
이 때 N 사용횟수의 최솟값을 리턴해야 한다.
접근 방법
다이나믹 프로그래밍 문제임을 알고 있어서 dp 테이블을 어떻게 정의해야 하는지 고민하다가 처음에는 다음과 같이 정의했다.
dp[i]: i를 만드는데 필요한 N의 최소 개수
N = 5일 때, dp[0] = 0, dp[1] = 5/5 → 2, … dp[5] = 1
그리고 점화식으로는, dp[i] = min(1~(i-1) 중 더해서 i가 되는 조합의 숫자에 해당하는 인덱스의 dp 값)
즉, dp[7] = min(dp[1] + dp[6], dp[2] + dp[5], ….)
이렇게 구현하려고 했으나, i가 되는 조합이 매우 많고 찾는데 시간이 걸려서 구현이 복잡했었다.
따라서 이 문제는 dp 테이블을 다음과 같이 정의 해야 한다.
dp[i] = N이 i개 있을 때 만들 수 있는 숫자 집합
이렇게 정의하면, dp 테이블에서 어떤 패턴을 찾을 수 있다.
N=5일 때,
dp[0] = {0}
dp[1] = {5}
dp[2] = {55, 5+5, 5/5, 5-5, 5*5}
dp[3] = {555, 5+5+5, 5+5-5, 5+5*5, 5+5/5, …}dp[3]을 잘 살펴보면, dp[1] 의 원소 - 사칙연산 - dp[2]의 원소 또는 dp[2] 의 원소 - 사칙연산 - dp[2]의 원소 임을 알 수 있다.
이런식으로 dp 테이블에 가능한 숫자들을 추가하고, 찾고자 하는 숫자가 dp[i]에 있다면, i가 최소 사용횟수가 된다.
또한 문제에서 최솟값이 8보다 크면 -1을 리턴한다고 했으므로, dp 테이블은 8까지만 생성해주면 된다.
문제 해설
- number가 1이라면, 1을 리턴해준다.
- dp 테이블을 만들어준다
- 1~8까지, ‘NN..’ 형태의 수를 각 dp 테이블에 넣어준다.
dp[1] 의 원소 - 사칙연산 - dp[2]의 원소또는dp[2] 의 원소 - 사칙연산 - dp[2]의 원소를 계산해서 부분집합에 추가해준다.
- 만약, 찾고자하는 number가 dp[i]의 부분집합에 속해있다면, 리턴해준다.
풀이
def solution(N, number):
if number == 1:
return 1
set_list = []
for cnt in range(1, 9): # 1개부터 8개까지 확인
partial_set = set()
partial_set.add(int(str(N) * cnt)) # 이어 붙여서 만드는 경우 넣기
for i in range(cnt - 1): # (1, n-1) 부터 (n-1, 1)까지 사칙연산
for op1 in set_list[i]:
for op2 in set_list[-i - 1]:
partial_set.add(op1 + op2)
partial_set.add(op1 * op2)
partial_set.add(op1 - op2)
if op2 != 0:
partial_set.add(op1 / op2)
# 만든 집합에 number가 처음 나오는지 확인
if number in partial_set:
return cnt
set_list.append(partial_set)
return -1
정리
- 어려운 문제였다…
- dp 테이블을 어떻게 정의해야하는지도 문제였지만, for문의 인덱스 설정하고 이해하는데 시간이 너무 오래걸렸다.
- 특히, set_list[i]와 set_list[-i-1] 부분에서 어려웠다.
- 리스트의 인덱싱이 능숙하지 않아서 더 오래걸린 것 같다.
Uploaded by N2T




